
dp[n][m] : n개의 수를 m개의 구간으로 나눴을 때 구간에 속한 수들의 최댓값
점화식을 세워보도록 하자
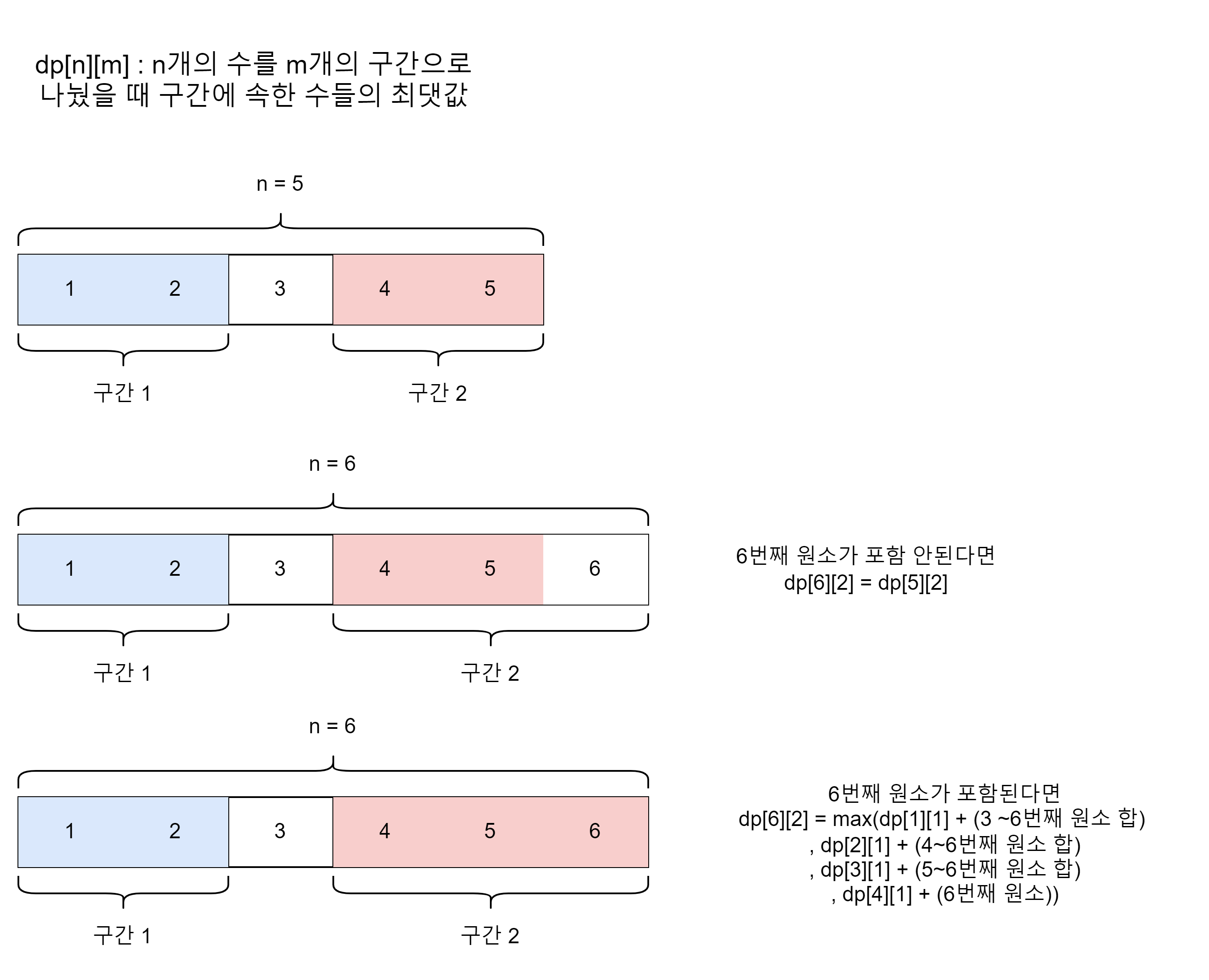
n개의 원소를 m개의 그룹으로 나눈다.
- n번째 원소가 포함이 안되는 경우 dp[n][m] = dp[n-1][m]
- n번째 원소가 포함되는 경우 dp[n][m] = max(dp[n-2][m-1] + (n번째 원소), dp[n-3][m-1] + (n-1 ~ n번째 원소 합), dp[n-4][m-1] + (n-2 ~ n번째 원소 합), .... , dp[1][m-1] + (3 ~ n번째 원소 합))
다만 여기서 원소합 계산을 편하게 하기 위해 누적합을 이용한다!
import java.io.*;
import java.util.*;
public class Main {
static BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
static BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
static StringTokenizer st;
public static void main(String[] args) throws IOException {
// 5:45
st = new StringTokenizer(br.readLine());
int N = Integer.parseInt(st.nextToken());
int M = Integer.parseInt(st.nextToken());
int[] sum = new int[N+1];
int[][] dp = new int[N+1][M+1];
for(int i = 0; i < N; i++) {
st = new StringTokenizer(br.readLine());
sum[i+1] = sum[i] + Integer.parseInt(st.nextToken());
}
for(int i = 0; i <= N; i++) {
for(int j = 1; j <= M; j++) {
dp[i][j] = -32768 * 101;
}
}
dp[1][1] = sum[1];
for(int i = 2; i <= N; i++) {
for(int j = 1; j <= M; j++) {
dp[i][j] = dp[i-1][j];
// j == 1 이면 처음부터 i까지 원소 합도 고려해봐야하는데
// sum[i] - sum[k+1] 로는 첫번째 원소가 넣어질 방법이 없기 때문
if(j == 1) {
dp[i][j] = Math.max(dp[i][j], sum[i]);
}
for(int k = 0; k <= i-2; k++) {
dp[i][j] = Math.max(dp[i][j], dp[k][j-1] + sum[i] - sum[k+1]);
}
}
}
// print(dp);
bw.write(dp[N][M]+"");
bw.flush();
}
static void print(int[][] dp) {
for(int i = 0; i < dp.length; i++) {
for(int j = 0; j < dp[0].length; j++) {
System.out.print(String.format("%3d", dp[i][j]));
}
System.out.println();
}
}
}
knapsack 과는 무슨 차이였는지?
n개의 원소를 최대 무게 w인 가방에 넣었을 때의 가치 최댓값이번 문제가 개수에 제한이 있는 반면 knapsack 배낭 문제는 최대무게가 제한이 있다.
'🧩Algorithm' 카테고리의 다른 글
| [Algorithm] 2023 현대모비스 알고리즘 경진대회 예선 - 상담원 인원 (0) | 2023.08.31 |
|---|---|
| [Algorithm] 백준 5052 전화번호 목록 (트라이 풀이) (0) | 2023.08.05 |
| [Algorithm] 백준 2800 스택-구현 (0) | 2023.07.18 |
| [Algorithm] 백준 2629 양팔저울 (0) | 2023.07.06 |
| [Algorithm] 백준 12865 평범한 배낭 (0-1 knapsack) (0) | 2023.07.04 |
