중요한건 왜 dp인지 이해하는 것
dp[w][k] : 가방의 최대 무게가 w이고 k 번째 보석을 담을 때 갖을 수 있는 가치 최댓값
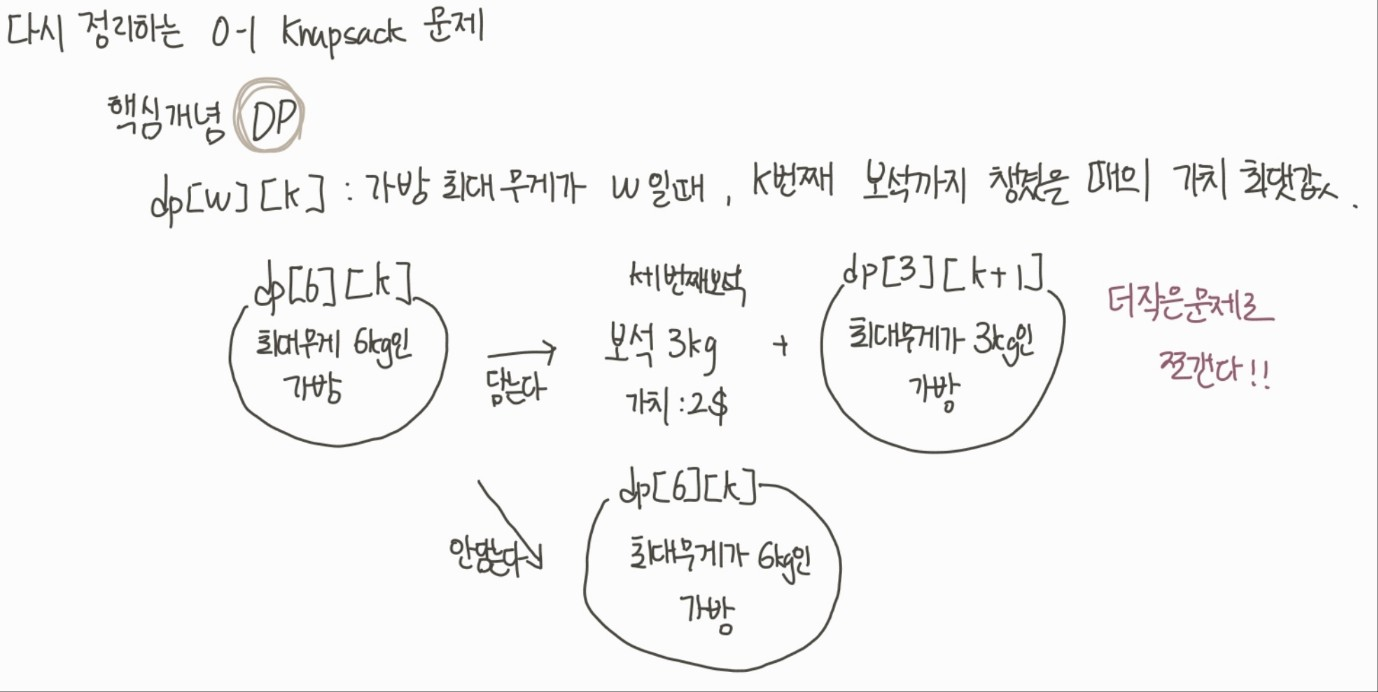
_(그림 오타 dp[3][k+1] -> dp[3][k])
예를 들어, 최대 무게가 6kg 이고 k번째 보석을 담은 상태라고 하자. 다음 보석을 담을 때의 점화식을 세워보자. (dp[6][k+1]) 그렇다면 k+1 번째 보석을 담을 수 있다면 담는다 or 안담는다 로 나눌 수 있다.
이때 안 담는다면 최대 무게가 6kg 이고 k 번째 보석을 담는 상태와 같다. 따라서
dp[6][k+1] = dp[6][k]
반대로 담는다면 dynamic programming 의 본질에 맞게 subproblem으로 쪼갤 수 있다.
k+1 번째 보석이 3kg 이다. 그렇다면 우리는 가방 최대 무게가 (6-3) kg 일때의 가치 최댓값에다가 넣으려는 보석의 가치를 그대로 더하면 된다.
dp[6][k+1] = dp[6-3][k] + (k+1번째 보석의 가치)
코드 정리
- dp 테이블 초기화 - w 나 k 가 0일때 dp[w][k] = 0
- 점화식
- 1 k 번째 보석을 담을 수 있는 경우 (가방 최대 무게 보다 작거나 같은 경우) - 담거나 담지 않는다. 둘 중 최댓값
- 2 k 번째 보석을 담지 못하는 경우 (가방 최대 무게 보다 큰 경우) - 담지 않는다.
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.io.OutputStreamWriter;
import java.util.*;
public class Main {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
int n = Integer.parseInt(st.nextToken());
int k = Integer.parseInt(st.nextToken());
int[][] dp = new int[k+1][n+1];
int[] w = new int[n+1];
int[] v = new int[n+1];
for(int i = 1; i <= n; i++) {
st = new StringTokenizer(br.readLine());
w[i] = Integer.parseInt(st.nextToken());
v[i] = Integer.parseInt(st.nextToken());
}
// dp 테이블 초기화
for(int i = 0; i <= k; i++) {
dp[i][0] = 0;
}
for(int j = 0; j < n; j++) {
dp[0][j] = 0;
}
for(int j = 1; j <= n; j++) {
for(int i = 1; i <= k; i++) {
if(w[j] > i) dp[i][j] = dp[i][j-1];
else dp[i][j] = Math.max(dp[i][j-1], dp[i-w[j]][j-1] + v[j]);
}
}
System.out.println(dp[k][n]);
}
}'🧩Algorithm' 카테고리의 다른 글
| [Algorithm] 2023 현대모비스 알고리즘 경진대회 예선 - 상담원 인원 (0) | 2023.08.31 |
|---|---|
| [Algorithm] 백준 5052 전화번호 목록 (트라이 풀이) (0) | 2023.08.05 |
| [Algorithm] 백준 2228 구간 나누기 (0) | 2023.07.29 |
| [Algorithm] 백준 2800 스택-구현 (0) | 2023.07.18 |
| [Algorithm] 백준 2629 양팔저울 (0) | 2023.07.06 |